C Graph implementation with adjacency list representation using structures: Data Structure Tutorial 1

This is a quick tutorial for implementing graph data structure with adjacency list representation. Once I was
 looking on the web to have a simple introductory tutorial on graphs, but unfortunately couldn’t find one 
simple enough. So I decided to write this.

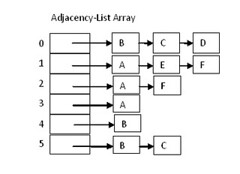
In the adjacency list representation,

è All the vertices are stored in an array of structure containing ‘data’ and ‘link’ fields.

è The linked chains represent the edges of a vertex with its neighbors.

In the figure, there are 6 vertices, represented by the array of length 6, and the chains represent the edges.

Below is another example:

Let us first define the structure of a vertex in a graph.

struct vertex

{

    int vertexKey;

    struct edge *edgePtr;

}vertex;

The vertexKey is the data field of the vertex, and edgePtr is the edge pointer, declared next.

The graph can be declared as:

struct vertex graph[10];

int vertexCount=0;

Here, we are taking the maximum number of vertices as 10.

The vertexCount gives us the number of vertices in the graph at a time.

Now, let us define the structure of an edge:

struct edge
{

    int vertexIndex;

    struct edge *edgePtr;

}edge;

Here, the vertexIndex field stores the index of the vertex to which the original vertex in the 
array is connected.

The following figure should make the structures clear:

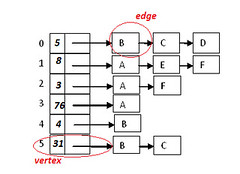
Inserting new vertex:

We have to insert a new vertex without any edges.

This can be implemented by incrementing the vertexCount and storing the vertex data in the 
graph array at vertexCount position.

void InsertVertex(int vertexKey)

{

    graph[vertexCount].vertexKey=vertexKey;

    graph[vertexCount].edgePtr=NULL;

    vertexCount++;

}

Note that the edgePtr of  the newly inserted vertex should point to NULL, i.e., it is a null 
pointer.

Now lets move on to insertion of an edge. The function is given below:

void insertEdge(int vertex1, int vertex2)

{

    struct edge *e,*e1,*e2;

     //For first vertex

    e=graph[vertex1].edgePtr;

    while(e&& e->edgePtr)

    {

        e=e->edgePtr;

    }

    e1=(struct edge *)malloc(sizeof(*e1));

    e1->vertexIndex=vertex2;

    e1->edgePtr=NULL;

    if(e)

    e->edgePtr=e1;

    else

    graph[vertex1].edgePtr=e1;

    

     //For second vertex

    e=graph[vertex2].edgePtr;

    while(e&& e->edgePtr)

    {

        e=e->edgePtr;

    }

    e2=(struct edge *)malloc(sizeof(*e2));

    e2->vertexIndex=vertex1;

    e2->edgePtr=NULL;

    if(e)

    e->edgePtr=e2;

    else

    graph[vertex2].edgePtr=e2;

}

For inserting an edge, we just move to the end of the linked list of the corresponding vertex, 
and insert new edge there. We have to do this for both the vertices.

And finally, here is the implementation for printing the graph:

 void printGraph()

{

    int i;

    struct edge *e;

    for(i=0;i<vertexCount;i++)

    {

        printf("%d(%d)",i,graph[i].vertexKey);

        e=graph[i].edgePtr;

        while(e)

        {

            printf("->%d",e->vertexIndex);

            e=e->edgePtr;

        }

        printf("\n");

    }

}

To summarize, the full code is given below:

#include<stdio.h>

#include<stdlib.h>

struct edge

{

    int vertexIndex;

    struct edge *edgePtr;

}edge;

struct vertex

{

    int vertexKey;

    struct edge *edgePtr;

}vertex;

struct vertex graph[10];

int vertexCount=0;

void InsertVertex(int vertexKey)

{

    graph[vertexCount].vertexKey=vertexKey;

    graph[vertexCount].edgePtr=NULL;

    vertexCount++;

}

void insertEdge(int vertex1, int vertex2)

{

    struct edge *e,*e1,*e2;

    e=graph[vertex1].edgePtr;

    while(e&& e->edgePtr)

    {

        e=e->edgePtr;

    }

    e1=(struct edge *)malloc(sizeof(*e1));

    e1->vertexIndex=vertex2;

    e1->edgePtr=NULL;

    if(e)

    e->edgePtr=e1;

    else

    graph[vertex1].edgePtr=e1;

    e=graph[vertex2].edgePtr;

    while(e&& e->edgePtr)

    {

        e=e->edgePtr;

    }

    e2=(struct edge *)malloc(sizeof(*e2));

    e2->vertexIndex=vertex1;

    e2->edgePtr=NULL;

    if(e)

    e->edgePtr=e2;

    else

    graph[vertex2].edgePtr=e2;

}

void printGraph()

{

    int i;

    struct edge *e;

    for(i=0;i<vertexCount;i++)

    {

        printf("%d(%d)",i,graph[i].vertexKey);

        e=graph[i].edgePtr;

        while(e)

        {

            printf("->%d",e->vertexIndex);

            e=e->edgePtr;

        }

        printf("\n");

    }

}

main()

{

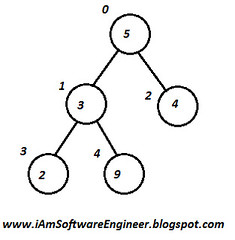
    InsertVertex(5);

    InsertVertex(3);

    InsertVertex(4);

    InsertVertex(2);

    InsertVertex(9);

    insertEdge(0,1);

    insertEdge(0,2);

    insertEdge(1,3);

    insertEdge(1,4);

    printGraph();

    return 0;

}

The ‘main’ function is for testing of the following graph:

And the final output is:

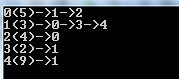
The data for each vertex is written in the braces.

Now, this implementation of graph is useful for almost all applications, but is not  optimum for 
‘delete vertex’ operation. For this, we will have to use a linked list instead of an array for 
storing the vertices. This is shown below:

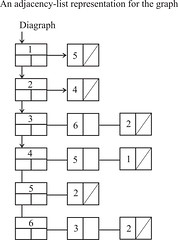
That completes our first tutorial on graphs. In the next tutorial, we will discuss graph 
operations like ‘depth-first-search’, ‘breadh-first-search’ etc.

If you have any queries or doubts, please ask through comments.


If you like this post, please consider to buy me a coffee.

Amount: $1.00 USD $3.00 USD $5.00 USD $10.00 USD $30.00 USD $50.00 USD $100.00 USD $200.00 USD $500.00 USD $1,000.00 USD

Don’t forget to subscribe this blog through email.